
It takes more space for storing sub matrices. It is not practically possible as it is computation and theoretical approach only. When the matrix is sparse this method works fine because sparse matrices take less time to compute. R2, c2 = r // 2, c// 2 return mat, mat, mat, matĬ = np.vstack((np.hstack((c11, c12)), np.hstack((c21, c22))))įrom the above we see that Strassen’s method is looking good, but it is good to remember is that it is not often used for matrix multiplication for five reasons:Ĭonstraints used in the above method are generally very large it takes more time in computation. In the first part we split our matrices into smaller matrices and in other functions we perform Strassen’s method of operation, which we see in the above formula of scalar addition and subtractions of the scalar.

MATRIX MULTIPLICATION DIVIDE AND CONQUER ALGORITHM CODE
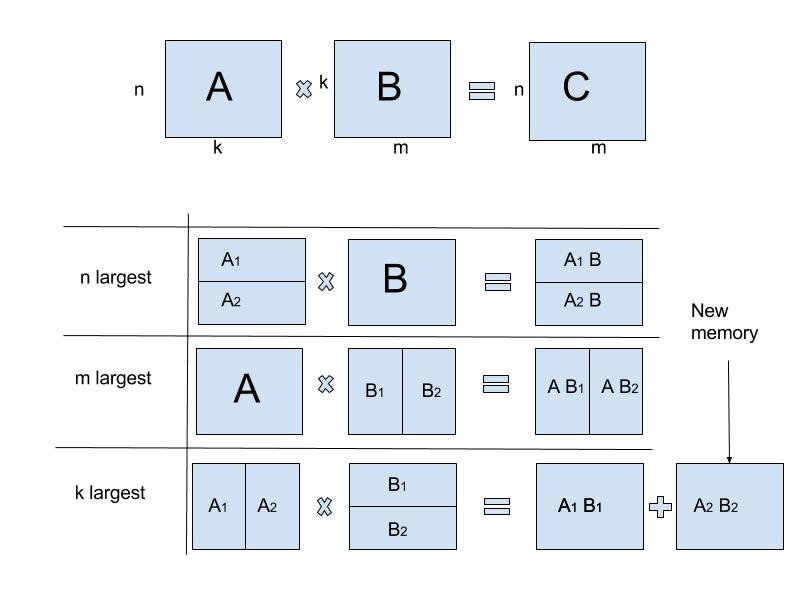
Pi=AiBi =(α1ia+α2ib+α3ic)(β1ie+β2if+β2ig) Where a,b ,β,α are the coefficients of the matrix that we see here, the product is obtained by just adding and subtracting the scalar.īelow is the code implementation using Python, divided into two parts. We do not exactly know why we take the row of one matrix A and column of the other matrix and multiply each by the below formula. Single IPython Notebook contains all Algorithms given in this Part 1. Submatrix Products: We have read many times how two matrices are multiplied. Now compute the r,s,t,u submatrices by just adding the scalars obtained from above points. Recursively compute the seven matrix products Pi=AiBi for i=1,2,…7. Using the formula of scalar additions and subtractions compute smaller matrices of size n/2. Steps of Strassen’s matrix multiplication:ĭivide the matrices A and B into smaller submatrices of the size n/2xn/2. It takes only seven recursive calls, multiplication of n/2xn/2 matrices and O(n^2) scalar additions and subtractions, giving the below recurrence relations. T(n)=O(n^3) Thus, this method is faster than the ordinary one. T(N) = 8T(N/2) + O(N2) From the above we see that simple matrix multiplication takes eight recursion calls. Using these equations to define a divide and conquer strategy we can get the relation among them as: Now from above we see: r=ae+bg s=af+bh t=ce+dg u=cf+dhĮach of the above four equations satisfies two multiplications of n/2Xn/2 matrices and addition of their n/2xn/2 products. We will divide these larger matrices into smaller sub matrices n/2 this will go on. Suppose we have two matrices, A and B, and we want to multiply them to form a new matrix, C.Ĭ=AB, where all A,B,C are square matrices. For larger matrices this approach will continue until we recurse all the smaller sub matrices. Here we divide our matrix into a smaller square matrix, solve that smaller square matrix and merge into larger results. Matrix multiplication is based on a divide and conquer-based approach.

The time complexity of this algorithm is O(n^(2.8), which is less than O(n^3). This article will focus on Strassen’s multiplication recursive algorithm for multiplying nxn matrices, which is a little faster than the simple brute-force method. Here we will use a memoization technique based on a divide and conquer approach. We also have fast algorithms using dynamic programming. Some are slow, like brute-force, in which we simply solve our problem with polynomial time. Volker Strassen first published this algorithm in 1969 and thereby proved that the n 3 so that matrices that are larger are more efficiently multiplied with Strassen's algorithm than the "traditional" way.We have seen a lot of algorithms for matrix multiplication. Strassen's algorithm works for any ring, such as plus/multiply, but not all semirings, such as min-plus or boolean algebra, where the naive algorithm still works, and so called combinatorial matrix multiplication.
For small matrices even faster algorithms exist. The Strassen algorithm is slower than the fastest known algorithms for extremely large matrices, but such galactic algorithms are not useful in practice, as they are much slower for matrices of practical size. It is faster than the standard matrix multiplication algorithm for large matrices, with a better asymptotic complexity, although the naive algorithm is often better for smaller matrices. Each of the 8 smaller matrix multiplications can themselves be performed in a divide-and-conquer style and so on till you get 1x1 matrices which can be. In linear algebra, the Strassen algorithm, named after Volker Strassen, is an algorithm for matrix multiplication.

Not to be confused with the Schönhage–Strassen algorithm for multiplication of polynomials.


 0 kommentar(er)
0 kommentar(er)
